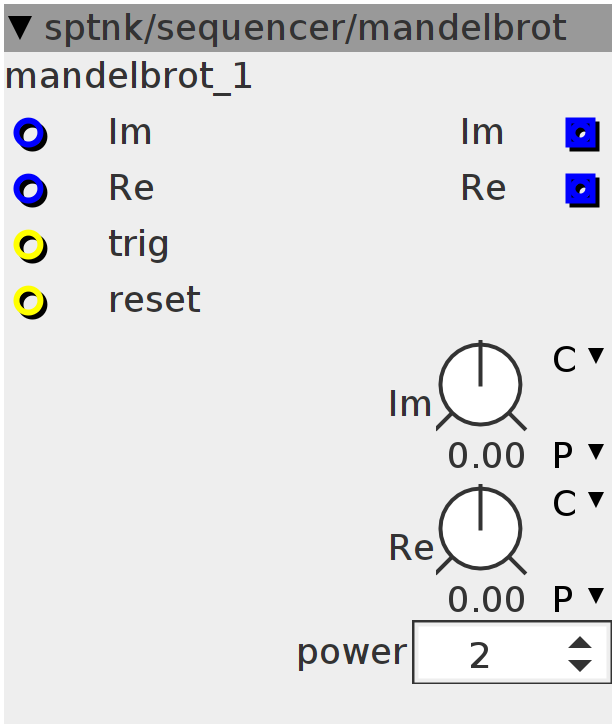
mandelbrot
Mandelbrot based iterator: generates a sequence of numbers iterating the fundamental mandelbrot equation z' = z^n +c , where z is the "old" number, n is an integer (>1) and c is a complex constant.
Inlets
bool32 Compute a new iteration
bool32 Reset
frac32 Imaginary part of the complex number c
frac32 Real part of the complex number c
Outlets
frac32 Imaginary part of the complex number z'
frac32 Real part of the complex number z'
Parameters
frac32.s.map Imaginary part of the complex number c
frac32.s.map Real part of the complex number c
int32 Power of the complex number z
int32_t Im_old = 0;
int32_t Re_old = 0;
int32_t a = 0;
int32_t b = 0;
int32_t c = 0;
int32_t d = 0;
bool rtrig = 0;
bool ttrig = 0;// main iterator block
//(ai + b)^n
//(ai + b)*(ci + d) = (ad+bc)i + (bd-ac)
// a_new = ad + bc
// b_new = bd - ac
if (inlet_trig && !ttrig) {
a = Im_old; // these two will be iterated
b = Re_old; // these two will be iterated
c = Im_old; // these two are constant through the cycles
d = Re_old; // these two are constant through the cycles
for (int i = 1; i < param_power; i++) {
a = ___SMMLA(b << 2, c << 3, ___SMMUL(a << 2, d << 3));
b = ___SMMLS(a << 2, c << 3, ___SMMUL(b << 2, d << 3));
}
Im_old = a + param_Im + inlet_Im;
Re_old = b + param_Re + inlet_Re;
ttrig = 1;
} else if (!inlet_trig)
ttrig = 0;
if (inlet_reset && !rtrig) {
rtrig = 1;
Im_old = 0;
Re_old = 0;
} else if (!inlet_reset)
rtrig = 0;
outlet_Im = Im_old;
outlet_Re = Re_old;