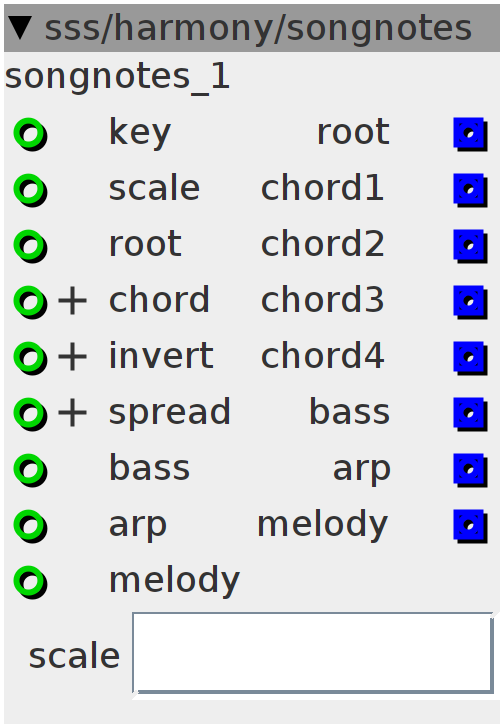
songnotes
46-scale scaling module for multiple oscillators. "root" sets the "rootnote" that will offset all the channels. "chord" sets the chord-spreading-variations throughout the scale. Max value...? unknown... "invert" creates different invertions of the chord. Max value...? unknown... "spread" spreads the chord by octaves in different combinations. Max value...? unknown... "bass" controls the bassline, available notes are the 4 notes used by the chord and perfect fifths above these up to 4 octaves, forced into the scale. "arp" and "melody" function in the same way, the inputs only offset the root. Chord-notes have no influence. All the generated notes will be scaled to the selected scale. 46! scales are included and each scale can be set to a key. See the Local Date for which scales are included. Scales are somewhat ordered on alphabetic orde (except the main major/minor scale variations which are the first ones). You can always set them to another order if you want, but keep the total at 46 as this selecting value gets wrapped above 46 in the code.
Inlets
int32 key
int32 scale
int32 root
int32 bass
int32 arp
int32 melody
int32.positive chord
int32.positive invert
int32.positive spread
Outlets
frac32 root
frac32 chord1
frac32 chord2
frac32 chord3
frac32 chord4
frac32 bass
frac32 arp
frac32 melody
Attributes
objref scale
int note;
int32_t scale(int NOTE, int SCALE, int KEY) {
int octave = NOTE / 12 - (NOTE < 0 ? 1 : 0);
int semitone = NOTE - octave * 12;
note = (attr_scale.note[semitone + SCALE * 12] + octave * 12 + KEY);
};
int ofs[4];
int32_t chord[4];
int i;int key = inlet_key - 4;
key = key - (key / 12) * 12;
key = key < 0 ? key + 12 : key;
int Scale = inlet_scale;
Scale = Scale - (Scale / 46) * 46;
Scale = Scale < 0 ? Scale + 46 : Scale;
for (i = 0; i < 4; i++) {
int j;
int k = 1 + (inlet_invert + 1) / 4;
j = i * k + inlet_invert;
j = j & 3;
int chord1 = (1 + inlet_chord >> 1) * j / 12;
int chord2 = (1 + inlet_chord >> 1) * j - chord1 * 12;
chord2 += chord1;
chord2 = chord2 - chord2 / 12 * 12;
j = j * inlet_spread;
int l = j / 3;
j += l;
j = j - j / 3 * 3;
j = j * 12;
ofs[i] = chord2 + j;
}
scale(inlet_root, Scale, key);
outlet_root = note << 21;
scale(inlet_root + ofs[0], Scale, key);
chord[0] = note;
outlet_chord1 = chord[0] << 21;
scale(inlet_root + ofs[1], Scale, key);
chord[1] = note;
outlet_chord2 = chord[1] << 21;
scale(inlet_root + ofs[2], Scale, key);
chord[2] = note;
outlet_chord3 = chord[2] << 21;
scale(inlet_root + ofs[3], Scale, key);
chord[3] = note;
outlet_chord4 = chord[3] << 21;
scale(inlet_root + chord[inlet_bass & 3] - chord[inlet_bass & 3] / 12 * 12 +
((inlet_bass >> 2) & 7) * 3.5,
Scale, key);
outlet_bass = note << 21;
scale(inlet_root + inlet_arp, Scale, key);
outlet_arp = note << 21;
scale(inlet_root + inlet_melody, Scale, key);
outlet_melody = note << 21;